和弦推导逻辑简析

诚然，吉他有上千个和弦。世界上最厉害的吉他大师，也无法一眼辨识出所有的和弦。

更多时候，我们熟记几个基本的和弦，然后通过一定的计算法则，去推导其他的和弦。因而推导的逻辑就非常重要。

《吉他三月通》一书把这乐理洋洋洒洒说了一百多页，我想试着让事情简单一些。

最后，我们将逻辑实现成一个小程序，可以方便打印出想要推导的和弦。

###音乐与数学

既然是逻辑，都可以用数学去建模，然而音乐与数学之间，却有一点非常重要的差异。

在这之前，我们得谈点有趣的事情，它们都有共同的原因：

1. 为什么我们会觉得某首歌很“中国风”？
2. 为什么某些日本的传统音乐听起来很“诡异”？
3. 为什么钢琴要做成黑键白键，所有键都一样不行吗？

我们常用——

正整数：1、2、3、4、5、6、7 ，
对应和弦：C、D、E、F、G、A、B，
对应音符：Do、Re、Me、Fa、So、La、Ti

每个正整数之间，都是相差1；而按频率高低排列的音符，由于历史原因，它们并不是等差数列。

实际上，4比理想的要低一点，7比理想的要高一点，其他的5个音，则基本在理想线性曲线上！

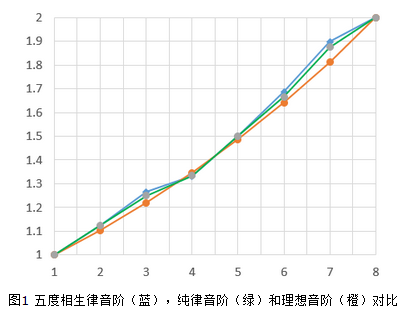
这5个跟理想比较吻合的音，就是天朝古代的五音阶：宫、商、角、徵、羽。“中国风”的歌曲，大多使用了这五个音，所以让人感到舒服和温和；而日本的传统音乐，反其道而行用了许多4与7（这么说也不太对，具体是受阴阳调式影响，但表现上大概如此），有一种幽静阴深的效果。

所以，以上问题的原因是：音符的递增不完全是线性的！

我们得把4和7这两个不和谐点标志出来，就出现了“半音和全音”的理论。
把3到4和7到1这两个不满一个跨度的叫做半音；其他相邻音符之间，都叫做全音。
而造物主的神奇之处在于：两个半音等于一个全音。

音乐的世界跟数学的这点不同，会在后面逻辑推导上会给我们一点小小的麻烦。

###音乐家与程序员

试想，如果程序员要完成描述音阶的数据结构，会如何设计呢？

通常，应该先规划“最小粒度”。而“半音”刚好是最合适的选择。

音乐家与程序员的处理方式如出一辙，钢琴上夹在两个白键之间的黑键，吉他相邻品丝之间，都是为了表现出半音。

如果用程序描述吉他品丝的关系就是：

var scale = [2, 2, 1, 2, 2, 2, 1];  //3-4是半音，7-1也是半音，相隔1品；其他是全音，相隔2品

###吉他与尺子

知道了这些，我们就好比掌握了一把尺子的刻度。

在尺子上，如果一个刻度表示1cm，那么从3cm往后推两个格子，就是5cm；
把吉他想象成尺子，一个刻度表示半音，和弦之间就可以推导了。

与众不同的是，这把尺子首尾相连，更像一个循环的圈。

刻度：    2品       2品       1品       2品       2品       2品       1品       2品       2品
和弦：C  +----> D  +----> E  +----> F  +----> G  +----> A  +----> B  +----> C  +----> D  +----> ……
音符：Do +----> Re +----> Me +----> Fa +----> So +----> La +----> Ti +----> Do +----> Re +----> ……
整数：1  +----> 2  +----> 3  +----> 4  +----> 5  +----> 6  +----> 7  +----> 1  +----> 2  +----> ……

因而，一个和弦可以有多种方式弹奏。
比如C和弦，除了最基础的开放式（不需要用食指横按品丝）指法，我们还可以用A和弦的指法实现：

C = B + 1品
  = A + 2品 + 1品
  = A + 3品

所以，我们用食指横按住第3品（或者用变调夹夹第3品），然后再加上A和弦的开放式指法，就形成了一个C和弦。

同理也可以用E和弦实现：

C = B + 1品
  = A + 2品 + 1品
  = G + 2品 + 2品 + 1品
  = F + 2品 + 2品 + 2品 + 1品
  = E + 1品 + 2品 + 2品 + 2品 + 1品
  = E + 8品

横按的位置就在第8品上。

其实大部分情况下，我们都是用A，E，Am，Em这四个和弦去推导其他和弦，因为这几个和弦横按与转换比较方便，特别是在扫弦的时候。

###程序实现

明确逻辑之后，就差程序实现了。但这之前，我们定了程序的最小粒度是1品，就无可避免遇到一个问题：

如果A + 2品 = B，那A + 1品 = ？

这个和弦介于A与B之间，人们把它称为升A或降B，对应记法是A#或Bb。

至此我们可以列出，用E指法和A指法推导的所有和弦的横按位置：

var positions = {
    "E": {
    	"A":  5,
    	"A#": 6,
    	"Bb": 6,
    	"B":  7,
    	"C":  8,
    	"C#": 9,
    	"Db": 9,
    	"D":  10,
    	"D#": 11,
    	"Eb": 11,
    	"E":  12,
    	"F":  1,
    	"F#": 2,
    	"Gb": 2,
    	"G":  3,
    	"G#": 4,
    	"Ab": 4
    },
    "A": {
     	"A":  12,
     	"A#": 1,
     	"Bb": 1,
     	"B":  2,
     	"C":  3,
     	"C#": 4,
     	"Db": 4,
     	"D":  5,
     	"D#": 6,
     	"Eb": 6,
     	"E":  7,
     	"F":  8,
     	"F#": 9,
     	"Gb": 9,
     	"G":  10,
     	"G#": 11,
     	"Ab": 11
    }
  };

同时，将E、A的开放和弦的指型描述出来：

//这里仅列出E、A大小和弦，共四种指法
//更详细指法数据结构可参看后面demo

chord_shapes = {
  	"M E": {
		name: "Maj",
		chord: [[3, 2], [4, 3], [5, 3]],
		bars: [{from_string: 6, to_string: 1, fret: 1}]
  	},
  	"m E": {
	    name: "m",
	    chord: [[4, 3], [5, 3]],
	    bars: [{from_string: 6, to_string: 1, fret: 1}]
  	},
  	"M A": {
	    name: "Maj",
	    chord: [[2, 3], [3, 3], [4, 3], [6, "x"]],
	    bars: [{from_string: 5, to_string: 1, fret: 1}]
  	},
  	"m A": {
	    name: "m",
	    chord: [[2, 2], [3, 3], [4, 3], [6, "x"]],
	    bars: [{from_string: 5, to_string: 1, fret: 1}]
  	}
};

分别传递“和弦名”,“指法”，“类型”作为参数，我们就可以很容易的画出和弦：

createChord("C", "A", "M A");  \\画出C和弦，用A指法，定义类型是大三和弦(Maj)
createChord("D", "A", "m A");  \\画出Dm和弦，用A指法，定义类型是小三和弦(Minor)

###Demo

以下是完整Demo，将上述chord_shapes的指型补充得更完整。

并且尝试用A指型，自动生成了C调的7个常用和弦。

End. 2015.5.25